Reinforcement Learning - Solving a Maze

As part of the master's course DeepLearning in the summer semester of 2022, various reinforcement learning algorithms were implemented using the Python programming language. The goal of the project was to solve a child's cube, or later a maze.

The code for the project is available on GitHub.

TL; DR;

Q-Table and Deep-QNetwork agents were implemented as part of the project. Very good results were achieved with the Q-Table approach and the agent quickly learns to play both games. The Deep-Q-Network agent only achieves small training successes and had serious performance problems at the beginning. With an optimized version, these could be solved, but unfortunately not the game's success. In addition, the project includes a graphical representation of the maze game that can be used to observe the gameplay. With a Docker Compose script, the project can also be run on powerful university servers (HSKL Skynet). The training and game results are mapped in the form of a graph using Matplotlib and can then be saved as a PNG file.

Cube

The subject of this game is a cube that has different shapes on its sides with an associated figure. The goal is to place all the figures on the corresponding sides of the cube in as few steps as possible. In our abstraction of the game, the order of the available figures is predetermined. The player can only rotate the cube (2-dimensionally) to the left or the right, or make several rotations simultaneously. The player has to also rotate the figure so that it fits into the corresponding shape of the side of the cube. Once all the figures have been placed in the cube by the player, the game is over.

Maze

In the maze, the player has to collect different targets in as few steps as possible. The player always starts the game from the same position and always has at least one chance to reach all the targets in the maze. Once the player has collected all the targets within the maze, the game is completed.

Reinforcement Learning

In reinforcement learning, an agent is exposed to a specific environment in which it can perform actions. The agent receives rewards based on its actions. With different return values of the rewards after an executed action, the agent is told whether the action should be interpreted as good or bad. For example, in our maze game, the agent is rewarded with a high reward if one of the targets is collected. Running into a wall on the other hand, the agent is punished with a negative reward.

There are different approaches to reinforcement learning algorithms. In this course, however, the focus is on Q-learning with Q-Table and the Deep Q-Network algorithm. These are to be considered completely independent of the environment, the actions, or the rewards. They only influence the approach of the agent.

Q-Learning with Q-Table

Another important component of Q-learning is the state. The state reflects the current state of the agent in the environment. In Q-learning, value pairs are now formed between the current state and the associated action (which causes the state). These reflect the quality of the action and are stored as so-called Q-Values in the Q-Table. In the beginning, the Q-table is initialized with 0 at every position. Finally, after each action, the agent updates the associated value in the Q-table with the following function rule:

updated_qvalue = (1 - alpha) * current_qvalue + alpha * (reward + gamma * max_value)

In this function rule, in addition to the now already known current Q-Value and the Reward, some unknown variables can be recognized. Alpha is the learning rate (value between 0 and 1) and determines the speed at which the agent learns the game. If the value is too large, performance suffers and oscillating results can occur, especially in training. If the learning rate is too small, the agent may get stuck at a result that does not match the optimum, or may not converge at all.

Gamma describes the weighting of future rewards (value between 0 and 1). For large values, rewards further in the future are weighted more heavily than imminent values. The last unknown, the maximum value of the table, is multiplied by Gamma to adjust the weighting to the current table.

Furthermore, when training the agent, an additional parameter Epsilon (value between 0 and 1) is typically introduced. This is used to intentionally not execute the action with the maximum reward with a certain probability, but instead perform a random action. This prevents the agent from specializing too early on a certain solution path without having tried other possibilities. With appropriately selected parameters, playing a trained Q-Table agent finally looks something like this:

(Note: A small problem in the renderer causes the last target collected not to be displayed).

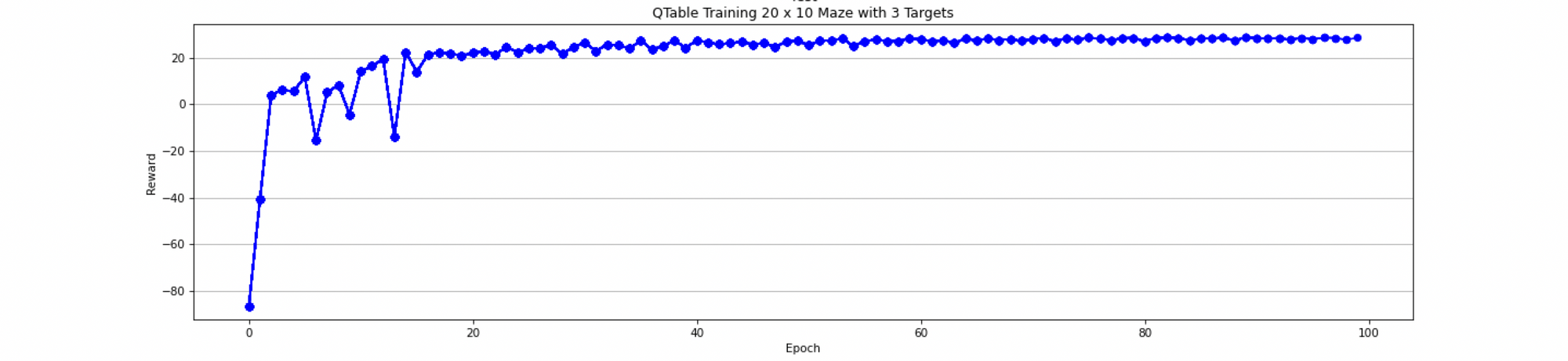
In the video above, the Q-Table agent plays the maze (20 x 10 with 3 targets) with the following parameters:

• Alpha=0.2
• Gamma = 0.8
• Epsilon = 0.1

After about 20 training episodes, the agent always achieves the maximum reward with these settings. The agent, therefore, learns very quickly to solve the game. In larger games, training takes much longer and the parameters should also be adjusted. Especially in very large games with more goals, it is recommended to adjust the learning rate, since the risk of perceiving a suboptimal solution path as the optimum increases here.

Deep Q-Network

Unlike the Q-Table agent, the Q-Network agent determines the next state using probability values determined by a Deep Neural Network. Like the Q-Table agent, the DQN agent learns to interact with its environment better over time and can thus make better decisions in the future based on experience from previous states.

The main difference between the Q-Table agent in the DQN agent is the retrain method. Here, a neural network from Tensorflow is used to retrain the agent. In the following example, the Tensorflow model was once again encapsulated in its class to be able to work directly with the state and action objects.

Specifically, the network contains two layers with 50 neurons each, which are activated with the ReLU function. The Mean Squared Error function is used as the loss function. Finally, an optimizer is added to the network, in our case an Adam optimizer with a learning rate of 0.01

model = Sequential()
model.add(Embedding(self._state_size, 10, input_length=1))
model.add(Reshape((10,)))
model.add(Dense(50, activation='relu'))
model.add(Dense(50, activation='relu'))
model.add(Dense(self._action_size, activation='linear'))

model.compile(loss='mse', optimizer=self._optimizer)

The retrain method randomly selects several moves from the game history, which can be configured via the batch size, with which the model is to be trained. With a prediction (predict) of the next action on a given state, an additional probability is an output. If the move has completed the game, the full reward is given to the action. If the game does not end, a prediction of the target network for the next state is offset against the current reward. The training network is re-trained with the state and the calculated rewards.

After every 10 past game weeks, the weights of the training network are transferred to the target network:

def retrain(self, batch_size):
    minibatch = random.sample(self.experience_replay, batch_size)

    for state, action, reward, next_state, terminated in minibatch:
        target_action, q_values = self.q_network.predict(state)

        if terminated:
            q_values[0][action.id] = reward
        else:
            t_action, t = self.target_network.predict(next_state)
            q_values[0][action.id] = reward + self.gamma * np.amax(t)

        self.q_network.fit(state, q_values, epochs=1, verbose=1)


def train(self, num_of_episodes, batch_size=100):
    for e in range(0, num_of_episodes):
        state = self.environment.reset_state()
        sum_reward = 0

        for timestep in range(self.timesteps_per_episode):
            action = self.act(state)
            next_state, reward, terminated, info = self.environment.step(action)
            sum_reward += reward
            self.store(state, action, reward, next_state, terminated)
            state = next_state

            if terminated:
                self.target_network.algin_model(self.q_network)
                break

            if len(self.experience_replay) > batch_size:
                self.retrain(batch_size)

        self.notify_writer_training((self.total_episodes, sum_reward))
        self.total_episodes += 1

        if (e + 1) % 10 == 0:
            self.target_network.algin_model(self.q_network)

The above game variant performs a prediction after every move, which is why the performance was severely affected. Therefore, another variant of the agent was implemented, which completely passes the game history to Tensorflow. Here it is important to pass the number of epochs and game steps so that the same training behavior is generated in the network.

def retrain(self, batch_size):
    batch = np.array(self.experience_replay)
    q_model = self.q_network.get_model()
    t_model = self.target_network.get_model()

    # Generate predictions for samples
    states = batch[:, 0]
    target = q_model.predict(states, steps=len(states))

    rows_terminated = np.where(batch[:, 4] == True)
    rewards_terminated_states = batch[rows_terminated][:, 2]
    action_indizes = np.argmax(target[rows_terminated], axis=1)
    target[:, action_indizes] = rewards_terminated_states

    rows_not_terminated = np.where(batch[:, 4] == False)
    rewards_not_terminated_states = batch[rows_not_terminated][:, 2]
    next_states = batch[rows_not_terminated][:, 3]
    t = t_model.predict(next_states, steps=len(next_states))

    action_indizes = np.argmax(target[rows_not_terminated], axis=1)
    target[:, action_indizes] = rewards_not_terminated_states + self.gamma * np.amax(t)
    
    q_model.fit(states, target, epochs=self.episodes_in_history, steps_per_epoch=self.timesteps_per_episode, verbose=0)

This performance-optimized variant processes the entire game history and instead of a batch_size the value timesteps_per_episode defines the maximum size of the game epoch. Another value determines the size of history. With the help of these parameters, the size of the histrory as well as the size of the episodes can be controlled. The prediction iterations, as well as the fit iterations, can be delegated directly to Tensorflow via the parameters. This optimization has made the retrain method significantly faster overall.

Software architecture

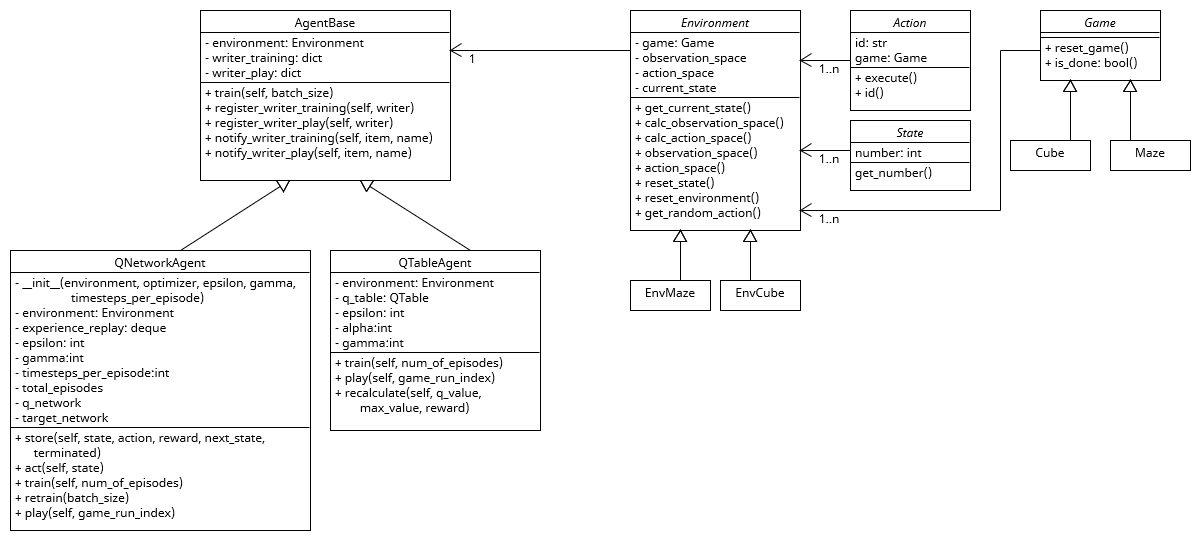
As shown in the class diagram above, the project was built using abstract parent classes and inheritance. The great advantage of this structure is that both the game or environment and the agent can be substituted at any time. An additional adapter class can be used to attach a renderer to the maze, which draws the gameplay in a Tkinter window. Furthermore, the extensibility is given by new games and agents.

The agents can also be initialized with different parameters. This gives us full flexibility over the agents and their environment. This flexibility was used to read in fully-automated test suites that contain a pre-built configuration and automatically configure the agent and environment accordingly. The configuration file is created in JSON format and has the following form:

{
    "result_path": "./var/results/",
    "testsuite_name": "Testsuite_1",
    "deactivated": false,
    "agent": {
        "type": "QNetworkAgent",
        "learning_rate": 0.005,
        "train_epochs": 50,
        "timesteps_per_episode": 100,
        "gamma": 0.9,
        "epsilon": 0.3,
        "batch_size": 50
    },
    "play": {
        "number_of_plays": 100
    },
    "maze": {
        "height": 6,
        "width": 6,
        "targets": 3,
        "seed": 1337
    }
}

In result_path the results are saved as PNG files in the form of Matplotlib graphs. With the deactivated flag you can temporarily deactivate individual test suites. The agent receives all relevant parameters and also the type of the agent. For example, QTable could be specified here. The number_of_plays configures how often the agent should play. Finally, the maze contains the configuration for the size of the maze and the number of targets. Alternatively, the game cube with the attribute facesize can be specified at this point.

Several JSON configuration files can now be stored in the test suite. The configurations are read in advance and then executed one after the other. By saving the results as a PNG file, the test suite can be easily executed in the background with different configurations.

With the test setup, training runs with different configurations can now be easily started without having to manually observe the application. This means that the project can no longer be started only locally, but also on a server. To create an environment on the server where the Python project can run with all package dependencies, we use Docker.

Conclusion

The Q-learning with the Q-table worked very well with both games. As shown in the example above, the algorithm is very fast in finding the maximum reward. The Q-learning with the DQN unfortunately does not work properly. Despite different configurations and adjusting the parameters, no useful learning curve could be generated.

In general, the project is nevertheless very well maintained and also easily extendable. The modular software architecture keeps it open to add more agents, environments, and games to the project in the future. Also, testing in an isolated server environment (HSKL Skynet) makes it easy to try out the agents in different environments with different configurations. Due to the extended monitoring, the results can be easily evaluated and compared. Overall, the project can be considered a success, as the project group was able to learn a lot about Deep Learning and Reinforcement Learning despite the unsuccessful implementation of DQN. The practical examination and implementation of various programming concepts with Python and the additionally integrated libraries such as Matplotlib, NumPy, Tkinter, TensorFlow, etc. also contributed to the learning success within the framework of the project work.